AVL Tree


What is an AVL Tree?

An AVL tree is a subtype of binary search tree. Named after it's inventors Adelson, Velskii and Landis, AVL trees have the property of dynamic self-balancing in addition to all the properties exhibited by binary search trees.

A BST is a data structure composed of nodes. It has the following guarantees:
  1. Each tree has a root node (at the top).
  2. The root node has zero, one or two child nodes.
  3. Each child node has zero, one or two child nodes, and so on.
  4. Each node has up to two children.
  5. For each node, its left descendants are less than the current node, which is less than the right descendants.
AVL trees have an additional guarantee:
  1. The difference between the depth of right and left subtrees cannot be more than one. In order to maintain this guarantee, an implementation of an AVL will include an algorithm to rebalance the tree when adding an additional element would upset this guarantee.
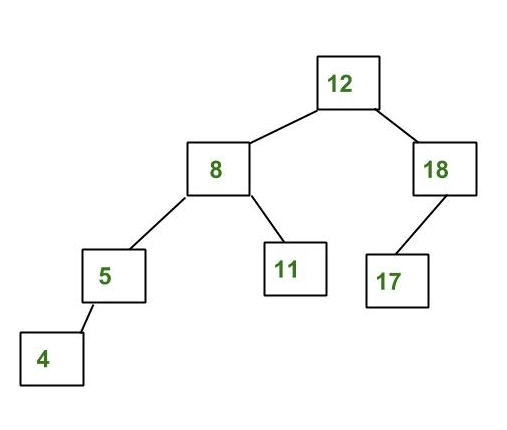
AVL trees have a worst case lookup, insert and delete time of O(log n).

An Example Tree that is an AVL Tree
(Source : geeksforgeeks.org)

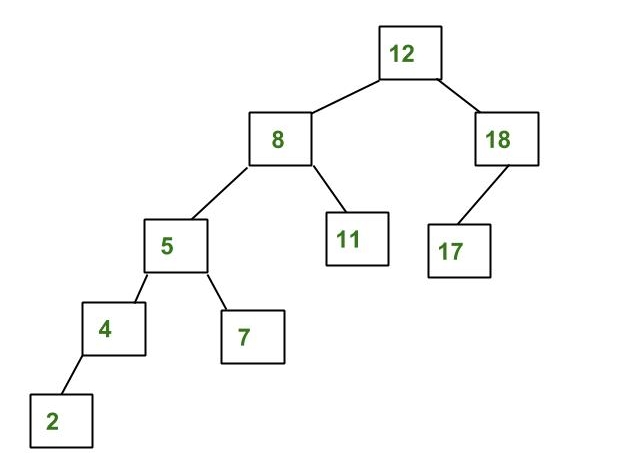
The above tree is AVL because differences between heights of left and right subtrees for every node is less than or equal to 1.


An Example Tree that is NOT an AVL Tree
(Source : geeksforgeeks.org)

The above tree is not AVL because differences between heights of left and right subtrees for 8 and 18 is greater than 1.

Why AVL Trees?
Most of the BST operations (e.g., search, max, min, insert, delete.. etc) take O(h) time where h is the height of the BST. The cost of these operations may become O(n) for a skewed Binary tree. If we make sure that height of the tree remains O(Logn) after every insertion and deletion, then we can guarantee an upper bound of O(Logn) for all these operations. The height of an AVL tree is always O(Logn) where n is the number of nodes in the tree.


Insertion
You will do an insertion similar to a normal Binary Search Tree insertion. After inserting, you fix the AVL property using left or right rotations.
  • If there is an imbalance in left child of right subtree, then you perform a left-right rotation.
  • If there is an imbalance in left child of left subtree, then you perform a right rotation.
  • If there is an imbalance in right child of right subtree, then you perform a left rotation.
  • If there is an imbalance in right child of left subtree, then you perform a right-left rotation.

AVL Tree Rotations

In AVL tree, after performing every operation like insertion and deletion we need to check the balance factor of every node in the tree. If every node satisfies the balance factor condition then we conclude the operation otherwise we must make it balanced. We use rotation operations to make the tree balanced whenever the tree is becoming imbalanced due to any operation.

Rotation operations are used to make a tree balanced.There are four rotations and they are classified into two types:

Single Left Rotation (LL Rotation)
In LL Rotation every node moves one position to left from the current position.

Single Right Rotation (RR Rotation)
In RR Rotation every node moves one position to right from the current position.

Left Right Rotation (LR Rotation)
The LR Rotation is combination of single left rotation followed by single right rotation. In LR Rotation, first every node moves one position to left then one position to right from the current position.

Right Left Rotation (RL Rotation)
The RL Rotation is combination of single right rotation followed by single left rotation. In RL Rotation, first every node moves one position to right then one position to left from the current position.


Time Analysis Of AVL Trees
AVL tree is binary search tree with additional property that difference between height of left sub-tree and right sub-tree of any node can’t be more than 1.

Algorithm Average Worst case: Space: O(n), Time: O(n)


Application of AVL Trees
AVL trees are beneficial in the cases where you are designing some database where insertions and deletions are not that frequent but you have to frequently look-up for the items present in there.
Source :

Komentar

Posting Komentar

Postingan populer dari blog ini

Heap and Tries

Gambar
What is HEAP? A heap is a tree-based data structure in which all the nodes of the tree are in a specific order. For example, if  X  is the parent node of  Y , then the value of  X  follows a specific order with respect to the value of  Y  and the same order will be followed across the tree. The maximum number of children of a node in a heap depends on the type of heap. However, in the more commonly-used heap type, there are at most  2  children of a node and it's known as a binary heap. In a binary heap, if the heap is a complete binary tree with  N  nodes, then it has the smallest possible height which is  l o g 2 N . Illustration of Heap In the diagram above, you can observe a particular sequence, i.e each node has greater value than any of its children. Suppose there are  N  Jobs in a queue to be done, and each job has its own priority. The job with maximum priority will get completed first than others. At each instant, we are completing a job with maxi
Baca selengkapnya
Gambar
Single Linked List First of all, what is Linked List? Linked List is pretty similar to array, but Linked List is  a linear data structure. Unlike arrays, linked list elements are not stored at a contiguous location; the elements are linked using pointers. ///Then, what is special about Linked Lists? Are they are just similar to Array?/// Even though array and linked lists are pretty similar, but there is some differences between arrays and linked lists. Here is the difference between array and linked list. What is Single Linked List? Single Linked List is a type of Linked Lists that only have a single pointer variable that points to the next element that will leads to the tail of Linked List, and the tail will points NULL.  here is the illustration of Single Linked List : P. S. : Head is the first element of Linked List and Tail is the last element of Linked List example of ' struct ' code : struct Scholar{       char name[25];  
Baca selengkapnya