Heap and Tries

What is HEAP?

A heap is a tree-based data structure in which all the nodes of the tree are in a specific order.

For example, if X is the parent node of Y, then the value of X follows a specific order with respect to the value of Y and the same order will be followed across the tree.

The maximum number of children of a node in a heap depends on the type of heap. However, in the more commonly-used heap type, there are at most 2 children of a node and it's known as a binary heap.

In a binary heap, if the heap is a complete binary tree with N nodes, then it has the smallest possible height which is log2N.

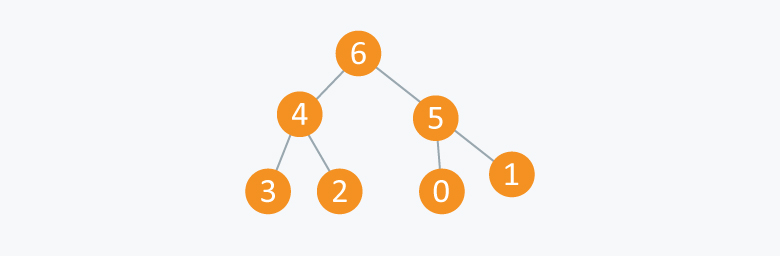
Illustration of Heap

In the diagram above, you can observe a particular sequence, i.e each node has greater value than any of its children.

Suppose there are $N$ Jobs in a queue to be done, and each job has its own priority. The job with maximum priority will get completed first than others. At each instant, we are completing a job with maximum priority and at the same time we are also interested in inserting a new job in the queue with its own priority.

So at each instant we have to check for the job with maximum priority to complete it and also insert if there is a new job. This task can be very easily executed using a heap by considering $N$ jobs as $N$ nodes of the tree.

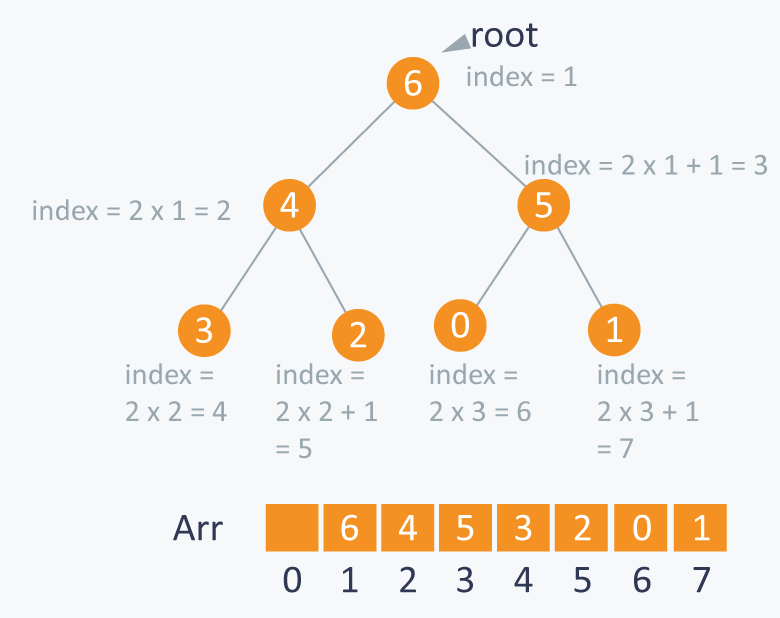
As you can see in the diagram below, we can use an array to store the nodes of the tree. Let’s say we have $7$ elements with values {6, 4, 5, 3, 2, 0, 1}.

Note: An array can be used to simulate a tree in the following way. If we are storing one element at index $i$ in array $Arr$, then its parent will be stored at index $i/2$ (unless its a root, as root has no parent) and can be accessed by $Arr[i/2]$, and its left child can be accessed by $Arr[2\ast i]$ and its right child can be accessed by $Arr[2\ast i+1]$. Index of root will be $1$ in an array.

There can be two types of heap:

Max Heap: In this type of heap, the value of parent node will always be greater than or equal to the value of child node across the tree and the node with highest value will be the root node of the tree.

Implementation:

Let’s assume that we have a heap having some elements which are stored in array $Arr$. The way to convert this array into a heap structure is the following. We pick a node in the array, check if the left sub-tree and the right sub-tree are max heaps, in themselves and the node itself is a max heap (it’s value should be greater than all the child nodes)

To do this we will implement a function that can maintain the property of max heap (i.e each element value should be greater than or equal to any of its child and smaller than or equal to its parent)

void max_heapify (int Arr[ ], int i, int N)
    {
        int left = 2*i                   //left child
        int right = 2*i +1           //right child
        if(left<= N and Arr[left] > Arr[i] )
              largest = left;
        else
             largest = i;
        if(right <= N and Arr[right] > Arr[largest] )
            largest = right;
        if(largest != i )
        {
            swap (Arr[i] , Arr[largest]);
            max_heapify (Arr, largest,N);
        } 
     }

Complexity: O(logN)

Building MAX HEAP:

Now let’s say we have $N$ elements stored in the array $Arr$ indexed from $1$ to $N$. They are currently not following the property of max heap. So we can use max-heapify function to make a max heap out of the array.

How?

From the above property we observed that elements from $Arr[N/2+1]$ to $Arr[N]$ are leaf nodes, and each node is a 1 element heap. We can use max_heapify function in a bottom up manner on remaining nodes, so that we can cover each node of tree.

void build_maxheap (int Arr[ ])
    {
        for(int i = N/2 ; i >= 1 ; i-- )
        {
            max_heapify (Arr, i) ;
        }
    }

Complexity: $O(N)$. max_heapify function has complexity $logN$ and the build_maxheap functions runs only $N/2$ times, but the amortized complexity for this function is actually linear.

For more details, you can refer this.

$<span\; style="background-color:\; black;\; color:\; white;\; font-family:\; "times"\; ,\; "times\; new\; roman"\; ,\; serif;"><br></span>$

$<span\; style="color:\; white;\; font-family:\; "helvetica\; neue"\; ,\; "arial"\; ,\; "helvetica"\; ,\; sans-serif;"></span>$

Min Heap: In this type of heap, the value of parent node will always be less than or equal to the value of child node across the tree and the node with lowest value will be the root node of tree.

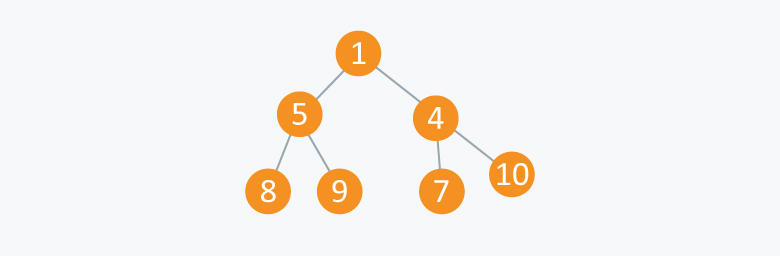
As you can see in the above diagram, each node has a value smaller than the value of their children.
We can perform same operations as performed in building max_heap.
First we will make function which can maintain the min heap property, if some element is violating it.

  void min_heapify (int Arr[ ] , int i, int N)
    {
    int left  = 2*i;
    int right = 2*i+1;
    int smallest;
    if(left <= N and Arr[left] < Arr[ i ] )
         smallest = left;
    else
        smallest = i;
    if(right <= N and Arr[right] < Arr[smallest] )
        smallest = right;
    if(smallest != i)
    {
        swap (Arr[ i ], Arr[ smallest ]);
        min_heapify (Arr, smallest,N);
    } 
    }

Complexity: $O(logN)$ .

APPLICATIONS:

1) Heap Sort:

We can use heaps in sorting the elements in a specific order in efficient time.
Let’s say we want to sort elements of array $Arr$ in ascending order. We can use max heap to perform this operation.

Idea: We build the max heap of elements stored in $Arr$, and the maximum element of $Arr$ will always be at the root of the heap.

Leveraging this idea we can sort an array in the following manner.

Processing:

• Initially we will build a max heap of elements in $Arr$.
• Now the root element that is $Arr[1]$ contains maximum element of $Arr$. After that, we will exchange this element with the last element of $Arr$ and will again build a max heap excluding the last element which is already in its correct position and will decrease the length of heap by one.
• We will repeat the step 2, until we get all the elements in their correct position.
• We will get a sorted array.

Implementation:

Suppose there are $N$ elements stored in array $Arr$.

 void heap_sort(int Arr[ ])
    {
        int heap_size = N;
        build_maxheap(Arr);
        for(int i = N; i>=2 ; i-- )
        {
            swap(Arr[ 1 ], Arr[ i ]);
            heap_size = heap_size-1;
            max_heapify(Arr, 1, heap_size);
        }
    }

Complexity: As we know max_heapify has complexity $O(logN)$, build_maxheap has complexity $O(N)$ and we run max_heapify $N-1$ times in heap_sort function, therefore complexity of heap_sort function is $O(NlogN)$.

2) Priority Queue:

Priority Queue is similar to queue where we insert an element from the back and remove an element from front, but with a difference that the logical order of elements in the priority queue depends on the priority of the elements. The element with highest priority will be moved to the front of the queue and one with lowest priority will move to the back of the queue. Thus it is possible that when you enqueue an element at the back in the queue, it can move to front because of its highest priority.

Priority Sort Illustration

We can think of many ways to implement the priority queue.

Naive Approach:
Suppose we have $N$ elements and we have to insert these elements in the priority queue. We can use list and can insert elements in $O(N)$ time and can sort them to maintain a priority queue in $O(NlogN)$ time.

Efficient Approach:
We can use heaps to implement the priority queue. It will take $O(logN)$ time to insert and delete each element in the priority queue.

Based on heap structure, priority queue also has two types max- priority queue and min - priority queue.

Let’s focus on Max Priority Queue.

Max Priority Queue is based on the structure of max heap and can perform following operations:

maximum(Arr) : It returns maximum element from the $Arr$.

extract_maximum (Arr) - It removes and return the maximum element from the $Arr$.

increase_val (Arr, i , val) - It increases the key of element stored at index $i$ in $Arr$ to new value val.

insert_val (Arr, val ) - It inserts the element with value val in Arr.

Implementation:

length = number of elements in Arr.

Maximum :

   int maximum(int Arr[ ])
        {
            return Arr[ 1 ];  //as the maximum element is the root element in the max heap.
        } 

Complexity: $O(1)$$<br>$

Extract Maximum: In this operation, the maximum element will be returned and the last element of heap will be placed at index 1 and max_heapify will be performed on node 1 as placing last element on index 1 will violate the property of max-heap.

    int extract_maximum (int Arr[ ])
    {
        if(length == 0)
        {
    cout<< “Can’t remove element as queue is empty”;
            return -1;
        }
        int max = Arr[1];
        Arr[1] = Arr[length];
        length = length -1;
        max_heapify(Arr, 1);
        return max;
    }

Complexity: $O(logN)$.

Increase Value: In case increasing value of any node, it may violate the property of max-heap, so we may have to swap the parent’s value with the node’s value until we get a larger value on parent node.

   void increase_value (int Arr[ ], int i, int val)
    {
        if(val < Arr[ i ])
        {
            cout<<”New value is less than current value, can’t be inserted” <<endl;
            return;
        }
        Arr[ i ] = val;
        while( i > 1 and Arr[ i/2 ] < Arr[ i ])
        {
            swap(Arr[ i/2 ], Arr[ i ]);
            i = i/2;
        }
    }

Complexity : $O(logN)$.

Insert Value :

 void insert_value (int Arr[ ], int val)
    {
        length = length + 1;
        Arr[ length ] = -1;  //assuming all the numbers greater than 0 are to be inserted in queue.
        increase_val (Arr, length, val);
    }

Complexity: $O(logN)$.

Example:

Initially there are 5 elements in priority queue.

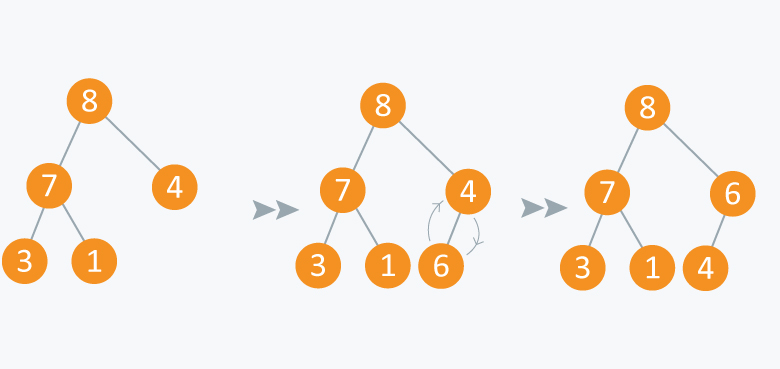
Operation: Insert Value(Arr, 6)

In the diagram below, inserting another element having value 6 is violating the property of max-priority queue, so it is swapped with its parent having value 4, thus maintaining the max priority queue.

Operation: Extract Maximum:
In the diagram below, after removing 8 and placing 4 at node 1, violates the property of max-priority queue. So max_heapify(Arr, 1) will be performed which will maintain the property of max - priority queue.

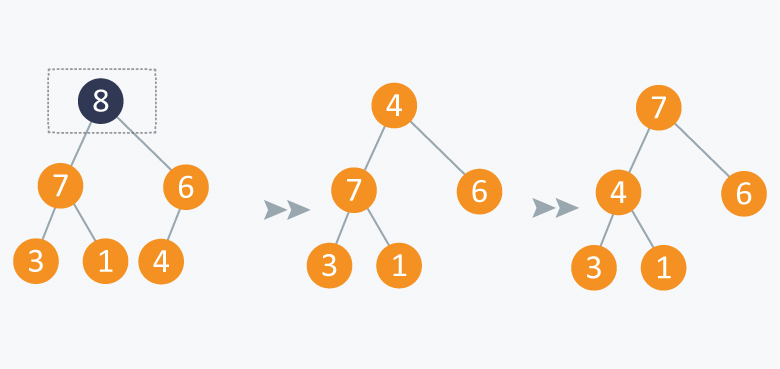
As discussed above, like heaps we can use priority queues in scheduling of jobs. When there are $N$ jobs in queue, each having its own priority. If the job with maximum priority will be completed first and will be removed from the queue, we can use priority queue’s operation extract_maximum here. If at every instant we have to add a new job in the queue, we can use insert_value operation as it will insert the element in $O(logN)$ and will also maintain the property of max heap.

TRIES

Trie is an efficient information reTrieval data structure. Using Trie, search complexities can be brought to optimal limit (key length). If we store keys in binary search tree, a well balanced BST will need time proportional to M * log N, where M is maximum string length and N is number of keys in tree. Using Trie, we can search the key in O(M) time. However the penalty is on Trie storage requirements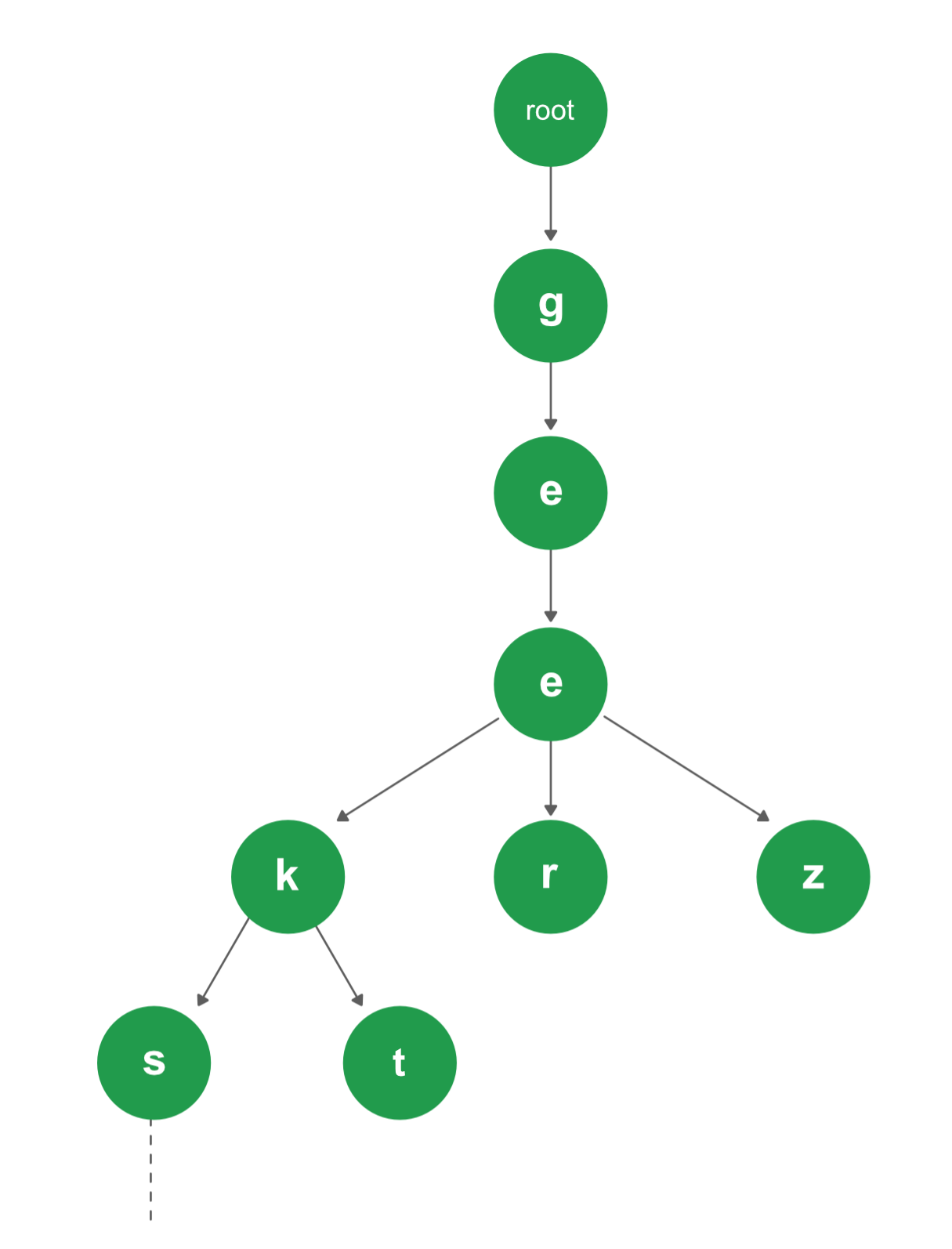

Every node of Trie consists of multiple branches. Each branch represents a possible character of keys. We need to mark the last node of every key as end of word node. A Trie node field isEndOfWord is used to distinguish the node as end of word node. A simple structure to represent nodes of the English alphabet can be as following,

// Trie node
struct TrieNode
{
     struct TrieNode *children[ALPHABET_SIZE];

     // isEndOfWord is true if the node
     // represents end of a word
     bool isEndOfWord;
};

Inserting a key into Trie is a simple approach. Every character of the input key is inserted as an individual Trie node. Note that the children is an array of pointers (or references) to next level trie nodes. The key character acts as an index into the array children. If the input key is new or an extension of the existing key, we need to construct non-existing nodes of the key, and mark end of the word for the last node. If the input key is a prefix of the existing key in Trie, we simply mark the last node of the key as the end of a word. The key length determines Trie depth.

Searching for a key is similar to insert operation, however, we only compare the characters and move down. The search can terminate due to the end of a string or lack of key in the trie. In the former case, if the isEndofWord field of the last node is true, then the key exists in the trie. In the second case, the search terminates without examining all the characters of the key, since the key is not present in the trie.

Insert and search costs O(key_length), however the memory requirements of Trie is O(ALPHABET_SIZE * key_length * N) where N is number of keys in Trie. There are efficient representation of trie nodes (e.g. compressed trie, ternary search tree, etc.) to minimize memory requirements of trie.

$<span\; style="font-family:\; "helvetica\; neue"\; ,\; "arial"\; ,\; "helvetica"\; ,\; sans-serif;"></span>$

Source :

1. https://www.hackerearth.com/practice/data-structures/trees/heapspriority-queues/tutorial/

2. https://www.geeksforgeeks.org/trie-insert-and-search/