Binary Search Tree
Binary Search Tree
Hello again, welcome at my blog. At this moment, I am going to talk about 'Binary Search Tree'. What is Binary Search Tree? Is it same with Binary Tree? I will explain all of them here.
What is Binary Search Tree?
Binary search tree is a data structure that quickly allows us to maintain a sorted list of numbers.
What is Binary Search Tree?
Binary search tree is a data structure that quickly allows us to maintain a sorted list of numbers.
- It is called a binary tree because each tree node has maximum of two children.
- It is called a search tree because it can be used to search for the presence of a number in O(log(n)) time.
- All nodes of left subtree are less than root node
- All nodes of right subtree are more than root node
- Both subtrees of each node are also BSTs i.e. they have the above two properties
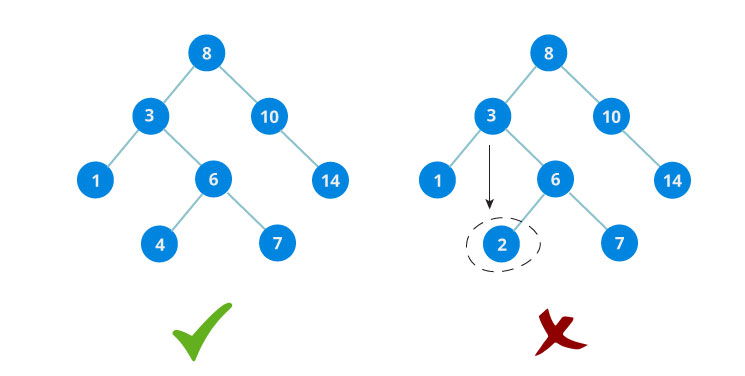
The binary tree on the right isn't a binary search tree because the right subtree of the node "3" contains a value smaller that it.
Is Binary Search Tree and Binary Tree just the same thing?
Actually, both of them are pretty similar but they have their own usage. A Binary Tree follows one simple rule that each parent node has no more than two child nodes, whereas a Binary Search Tree is just a variant of the binary tree which follows a relative order to how the nodes should be organized in a tree. You can read more of them here.
Basic Operations in Binary Search Tree
There is some basic operations that you can use in Binary Search Tree
1. Checking if number is present in Binary Search Tree
The algorithm depends on the property of BST that if each left subtree has values below root and each right subtree has values above root.
If the value is below root, we can say for sure that the value is not in the right subtree; we need to only search in the left subtree and if the value is above root, we can say for sure that the value is not in the left subtree; we need to only search in the right subtree.
Algorithm:
If root == NULL
return NULL;
If number == root->data
return root->data;
If number < root->data
return search(root->left);
If number > root->data
return search(root->right);
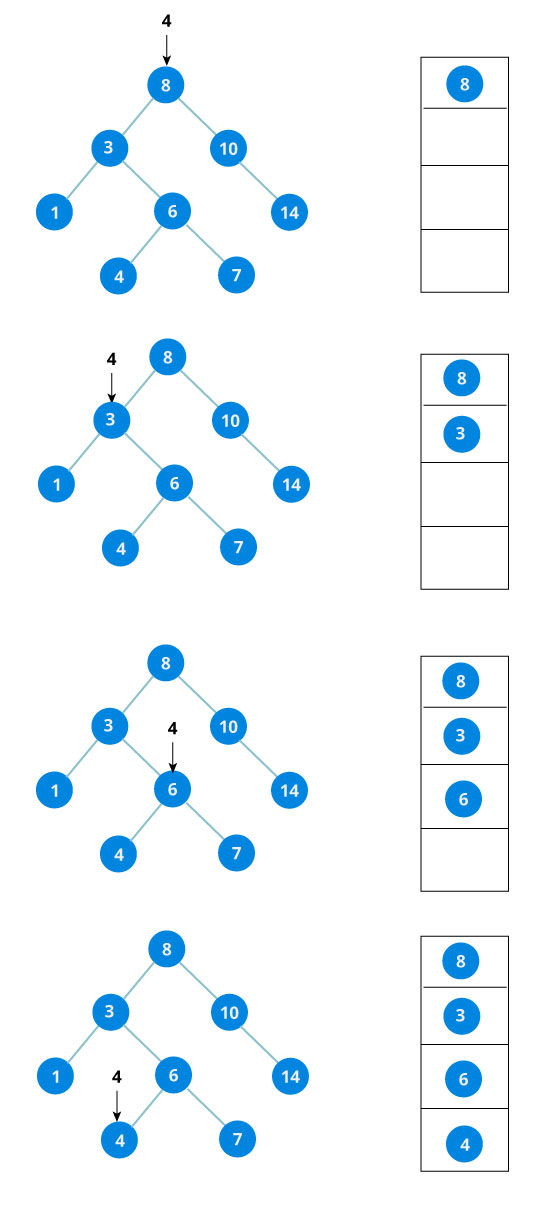
Let us try to visualize this with a diagram.
If the value is found, we return the value so that it gets propogated in each recursion step as shown in the image below.
If you might have noticed, we have called return search(struct node*) four times. When we return either the new node or NULL, the value gets returned again and again until search(root) returns the final result.
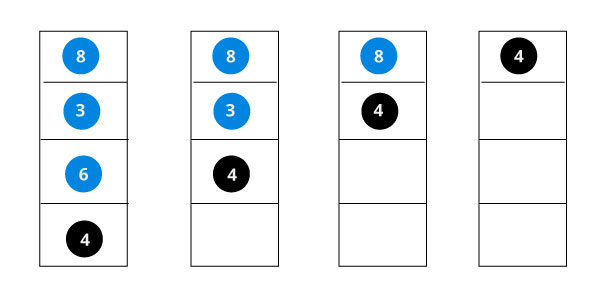
If the value is not found, we eventually reach the left or right child of a leaf node which is NULL and it gets propagated and returned.
Let us try to visualize this with a diagram.
If the value is found, we return the value so that it gets propogated in each recursion step as shown in the image below.
If you might have noticed, we have called return search(struct node*) four times. When we return either the new node or NULL, the value gets returned again and again until search(root) returns the final result.

If the value is not found, we eventually reach the left or right child of a leaf node which is NULL and it gets propagated and returned.
And here is the example in C
2. Insert value in Binary Search Tree(BST)
Inserting a value in the correct position is similar to searching because we try to maintain the rule that left subtree is lesser than root and right subtree is larger than root.
We keep going to either right subtree or left subtree depending on the value and when we reach a point left or right subtree is null, we put the new node there.
Algorithm:
Inserting a value in the correct position is similar to searching because we try to maintain the rule that left subtree is lesser than root and right subtree is larger than root.
We keep going to either right subtree or left subtree depending on the value and when we reach a point left or right subtree is null, we put the new node there.
Algorithm:
if node == NULL
return createNode(data)
if (data < node->data)
node->left = insert(node->left, data);
else if (data > node->data)
node->right = insert(node->right, data);
return node;
The algorithm isn't as simple as it looks. Let's try to visualize how we add a number to an existing BST.
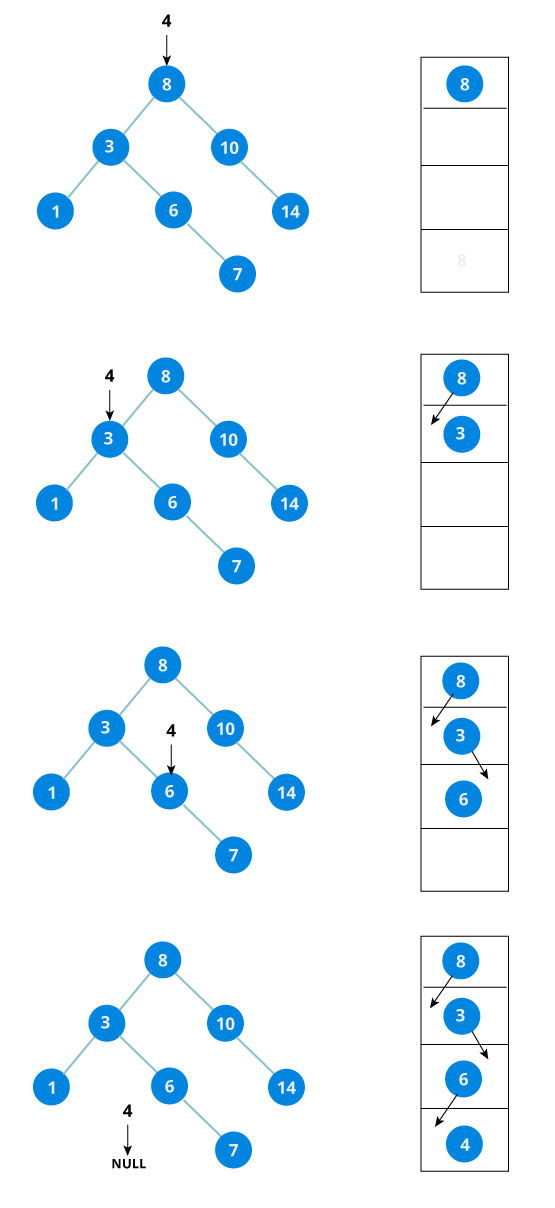
We have attached the node but we still have to exit from the function without doing any damage to the rest of the tree. This is where the return node; at the end comes in handy. In the case of NULL, the newly created node is returned and attached to the parent node, otherwise the same node is returned without any change as we go up until we return to the root.
This makes sure that as we move back up the tree, the other node connections aren't changed.
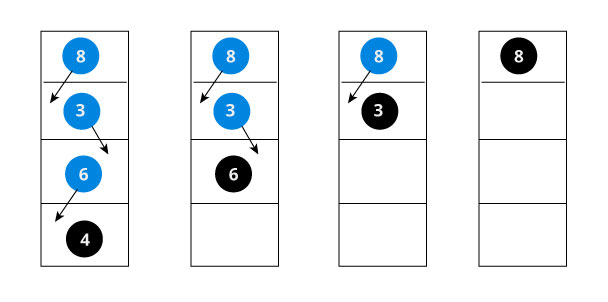
Time Complexity
The algorithm isn't as simple as it looks. Let's try to visualize how we add a number to an existing BST.

We have attached the node but we still have to exit from the function without doing any damage to the rest of the tree. This is where the return node; at the end comes in handy. In the case of NULL, the newly created node is returned and attached to the parent node, otherwise the same node is returned without any change as we go up until we return to the root.
This makes sure that as we move back up the tree, the other node connections aren't changed.

Here is the example code of insert value in BST in C:
The worst case time complexity of search and insert operations is O(h) where h is height of Binary Search Tree. In worst case, we may have to travel from root to the deepest leaf node. The height of a skewed tree may become n and the time complexity of search and insert operation may become O(n).
Some Interesting Facts
- Inorder traversal of BST always produces sorted output.
- We can construct a BST with only Preorder or Postorder or Level Order traversal. Note that we can always get inorder traversal by sorting the only given traversal.
- Number of unique BSTs with n distinct keys is Catalan Number
Source :
- http://www.differencebetween.net/technology/difference-between-binary-tree-and-binary-search-tree/
- https://www.programiz.com/dsa/binary-search-tree
- https://www.geeksforgeeks.org/binary-search-tree-set-1-search-and-insertion/




Komentar
Posting Komentar