Summary
Summary
The difference between array and linked list.
What is Single Linked List? Single Linked List is a type of Linked Lists that only have a single pointer variable that points to the next element that will leads to the tail of Linked List, and the tail will points NULL.
here is the illustration of Single Linked List :
P. S. : Head is the first element of Linked List and Tail is the last element of Linked List
example of 'struct' code :
struct Scholar{
char name[25];
int age;
struct Scholar *next;
}*head,*tail;
char name[25];
int age;
struct Scholar *next;
}*head,*tail;
Memory Allocation in Linked List
In C or C++ programming language, we could use 'malloc' for allocating the memory, and for delete the allocation memory we could use 'free'. The 'free' function usage is for clearing the memory allocation, but not the value of the element in Linked List.
Here is an example of malloc usage :
Insertion and Deletion of Nodes in Single Linked List
Insertion (also known as push) and deletion (also known as pop) is executed in the head, tail or even in the middle of linked list
- Insertion on Head of Linked List
This function is used for inserting or adding the element at the head of Linked List.
Here is the example of code for Insertion at Head :
Here is the example of code for Insertion at Head :
/// Insertion at Head of Linked List in C///
- Insertion on Tail of Linked List
This function is used for inserting or adding the element at the tail of Linked List.
Here is the example of code for Insertion at Tail :
Here is the example of code for Insertion at Tail :
/// Insertion at Tail of Linked List in C///
- Insertion at Middle of Linked List
This function is used for inserting or adding the element at the middle of Linked List.
Here is the example of code for Insertion at Middle :
Here is the example of code for Insertion at Middle :
/// Insertion at Middle of Linked List in C///
- Deletion at Head of Linked List
This function is used for deleting the element at the head of Linked List.
Here is the example of code for Deletion at Head :
Here is the example of code for Deletion at Head :
/// Deletion at Head of Linked List in C///
- Deletion at Middle of Linked List
This function is used for deleting the element at the middle of Linked List.
Here is the example of code for Deletion at Middle :
Here is the example of code for Deletion at Middle :
/// Deletion at Middle of Linked List in C///
- Deletion at Tail of Linked List
This function is used for deleting the element at the tail of Linked List.
Here is the example of code for Deletion at Tail :
Here is the example of code for Deletion at Tail :
/// Deletion at Tail of Linked List in C///
Double Linked List
Double Linked List is one of Linked List types that have 2 pointers. The one of the pointers points the next data and the other one points the previous data. If the existing data only one, both of pointers points the NULL.

Circular Linked List
Circular Linked List is one of Linked List types that the tail 'next' pointer doesn't points NULL, but points the head of Linked List. There are 2 types of Circular Linked List, those are the Circular Single Linked List and Circular Double Linked List.
• Circular Single Linked List
Illustration of Circular Single Linked List :
• Circular Double Linked List
Illustration of Circular Double Linked List :
Multiple Linked List
Multi Linked List a type of Linked List that have more than 2 pointers.
Illustration of Multiple Linked List :
Hashing
Hashing is an important Data Structure which is designed to use a special function called the Hash function which is used to map a given value with a particular key for faster access of elements. The efficiency of mapping depends of the efficiency of the hash function used.
Let a hash function H(x) maps the value x at the index x%10 in an Array. For example if the list of values is [11,12,13,14,15] it will be stored at positions {1,2,3,4,5} in the array or Hash table respectively.
As a simple example of the using of hashing in databases, a group of people could be arranged in a database like this:
Abernathy, Sara Epperdingle, Roscoe Moore, Wilfred Smith, David (and many more sorted into alphabetical order)
Each of these names would be the key in the database for that person's data. A database search mechanism would first have to start looking character-by-character across the name for matches until it found the match (or ruled the other entries out). But if each of the names were hashed, it might be possible (depending on the number of names in the database) to generate a unique four-digit key for each name. For example:
7864 Abernathy, Sara 9802 Epperdingle, Roscoe 1990 Moore, Wilfred 8822 Smith, David (and so forth)
A search for any name would first consist of computing the hash value (using the same hash function used to store the item) and then comparing for a match using that value. It would, in general, be much faster to find a match across four digits, each having only 10 possibilities, than across an unpredictable value length where each character had 26 possibilities.
The hash function is used to index the original value or key and then used later each time the data associated with the value or key is to be retrieved. Thus, hashing is always a one-way operation. There's no need to "reverse engineer" the hash function by analyzing the hashed values. In fact, the ideal hash function can't be derived by such analysis. A good hash function also should not produce the same hash value from two different inputs. If it does, this is known as a collision. A hash function that offers an extremely low risk of collision may be considered acceptable.
Here are some relatively simple hash functions that have been used:
- Division-remainder method: The size of the number of items in the table is estimated. That number is then used as a divisor into each original value or key to extract a quotient and a remainder. The remainder is the hashed value. (Since this method is liable to produce a number of collisions, any search mechanism would have to be able to recognize a collision and offer an alternate search mechanism.)
- Folding method: This method divides the original value (digits in this case) into several parts, adds the parts together, and then uses the last four digits (or some other arbitrary number of digits that will work ) as the hashed value or key.
- Radix transformation method: Where the value or key is digital, the number base (or radix) can be changed resulting in a different sequence of digits. (For example, a decimal numbered key could be transformed into a hexadecimal numbered key.) High-order digits could be discarded to fit a hash value of uniform length.
- Digit rearrangement method: This is simply taking part of the original value or key such as digits in positions 3 through 6, reversing their order, and then using that sequence of digits as the hash value or key.
Hash Tables
Hash Table is a data structure which stores data in an associative manner. In hash table, the data is stored in an array format where each data value has its own unique index value. Access of data becomes very fast, if we know the index of the desired data.
Basic Operations
Following are the basic primary operations of a hash table.
- Search − Searches an element in a hash table
- Insert − inserts an element in a hash table.
- delete − Deletes an element from a hash table.
DataItem
Define a data item having some data and key, based on which the search is to be conducted in a hash table.
Hash Method
Define a hashing method to compute the hash code of the key of the data item.
Search Operation
Whenever an element is to be searched, compute the hash code of the key passed and locate the element using that hash code as index in the array. Use linear probing to get the element ahead if the element is not found at the computed hash code.
Example
Insert Operation
Whenever an element is to be inserted, compute the hash code of the key passed and locate the index using that hash code as an index in the array. Use linear probing for empty location, if an element is found at the computed hash code.
Example
Delete Operation
Whenever an element is to be deleted, compute the hash code of the key passed and locate the index using that hash code as an index in the array. Use linear probing to get the element ahead if an element is not found at the computed hash code. When found, store a dummy item there to keep the performance of the hash table intact.
Example
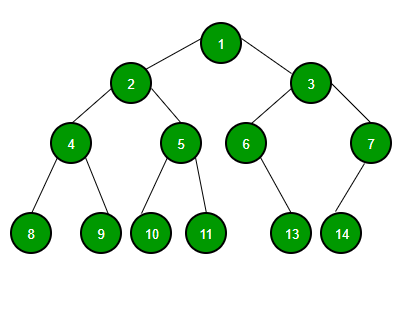
Binary Tree
A tree whose elements have at most 2 children is called a binary tree. Since each element in a binary tree can have only 2 children, we typically name them the left and right child.
Binary tree also known as B-tree.
A Binary Tree node contains following parts.
- Data
- Pointer to left child
- Pointer to right child
Example of Binary Tree Node
Search in B-Tree
To search a given key in Binary Search Tree, we first compare it with root, if the key is present at root, we return root. If key is greater than root’s key, we recur for right subtree of root node. Otherwise we recur for left subtree.
Insert in B-Tree
A new key is always inserted at leaf. We start searching a key from root till we hit a leaf node. Once a leaf node is found, the new node is added as a child of the leaf node.
Binary Search Tree
Hello again, welcome at my blog. At this moment, I am going to talk about 'Binary Search Tree'. What is Binary Search Tree? Is it same with Binary Tree? I will explain all of them here.
What is Binary Search Tree?
Binary search tree is a data structure that quickly allows us to maintain a sorted list of numbers.
What is Binary Search Tree?
Binary search tree is a data structure that quickly allows us to maintain a sorted list of numbers.
- It is called a binary tree because each tree node has maximum of two children.
- It is called a search tree because it can be used to search for the presence of a number in O(log(n)) time.
- All nodes of left subtree are less than root node
- All nodes of right subtree are more than root node
- Both subtrees of each node are also BSTs i.e. they have the above two properties
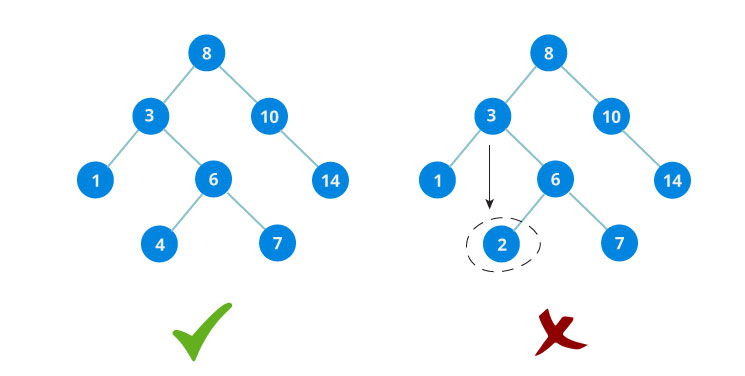
The binary tree on the right isn't a binary search tree because the right subtree of the node "3" contains a value smaller that it.
Is Binary Search Tree and Binary Tree just the same thing?
Actually, both of them are pretty similar but they have their own usage. A Binary Tree follows one simple rule that each parent node has no more than two child nodes, whereas a Binary Search Tree is just a variant of the binary tree which follows a relative order to how the nodes should be organized in a tree. You can read more of them here.
Basic Operations in Binary Search Tree
There is some basic operations that you can use in Binary Search Tree
1. Checking if number is present in Binary Search Tree
The algorithm depends on the property of BST that if each left subtree has values below root and each right subtree has values above root.
If the value is below root, we can say for sure that the value is not in the right subtree; we need to only search in the left subtree and if the value is above root, we can say for sure that the value is not in the left subtree; we need to only search in the right subtree.
Algorithm:
If root == NULL
return NULL;
If number == root->data
return root->data;
If number < root->data
return search(root->left);
If number > root->data
return search(root->right);
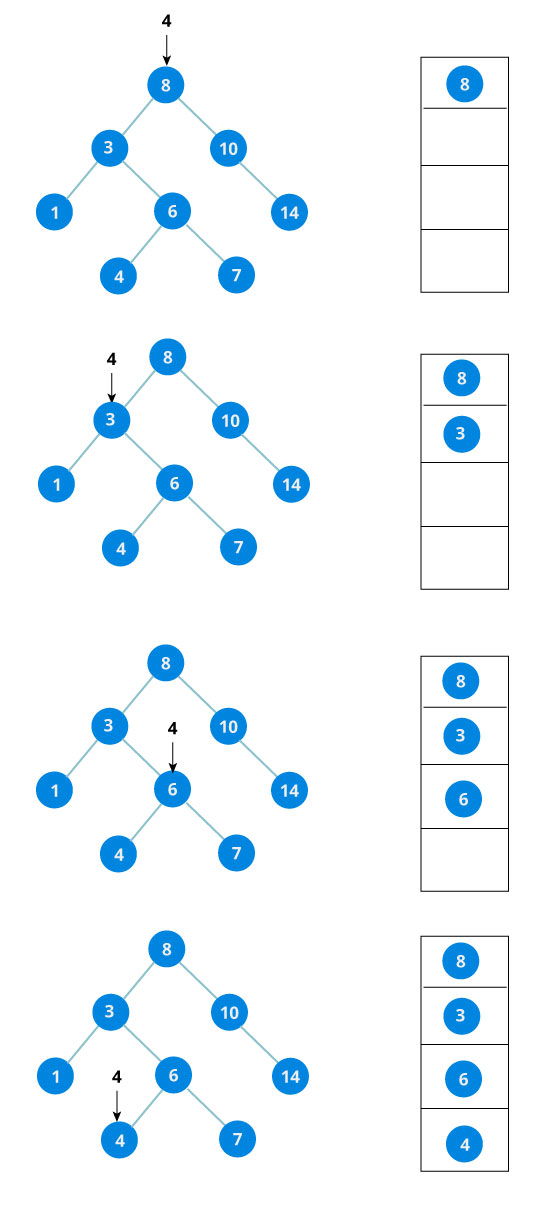
Let us try to visualize this with a diagram.
If the value is found, we return the value so that it gets propogated in each recursion step as shown in the image below.
If you might have noticed, we have called return search(struct node*) four times. When we return either the new node or NULL, the value gets returned again and again until search(root) returns the final result.
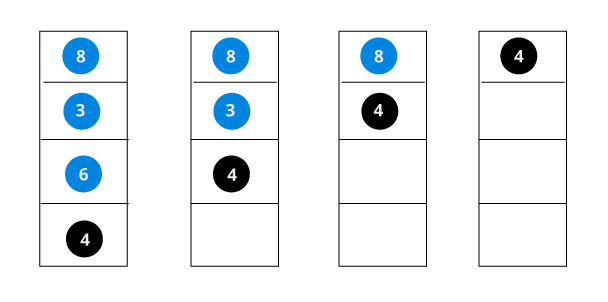
If the value is not found, we eventually reach the left or right child of a leaf node which is NULL and it gets propagated and returned.
Let us try to visualize this with a diagram.
If the value is found, we return the value so that it gets propogated in each recursion step as shown in the image below.
If you might have noticed, we have called return search(struct node*) four times. When we return either the new node or NULL, the value gets returned again and again until search(root) returns the final result.

If the value is not found, we eventually reach the left or right child of a leaf node which is NULL and it gets propagated and returned.
And here is the example in C
2. Insert value in Binary Search Tree(BST)
Inserting a value in the correct position is similar to searching because we try to maintain the rule that left subtree is lesser than root and right subtree is larger than root.
We keep going to either right subtree or left subtree depending on the value and when we reach a point left or right subtree is null, we put the new node there.
Algorithm:
Inserting a value in the correct position is similar to searching because we try to maintain the rule that left subtree is lesser than root and right subtree is larger than root.
We keep going to either right subtree or left subtree depending on the value and when we reach a point left or right subtree is null, we put the new node there.
Algorithm:
if node == NULL
return createNode(data)
if (data < node->data)
node->left = insert(node->left, data);
else if (data > node->data)
node->right = insert(node->right, data);
return node;
The algorithm isn't as simple as it looks. Let's try to visualize how we add a number to an existing BST.
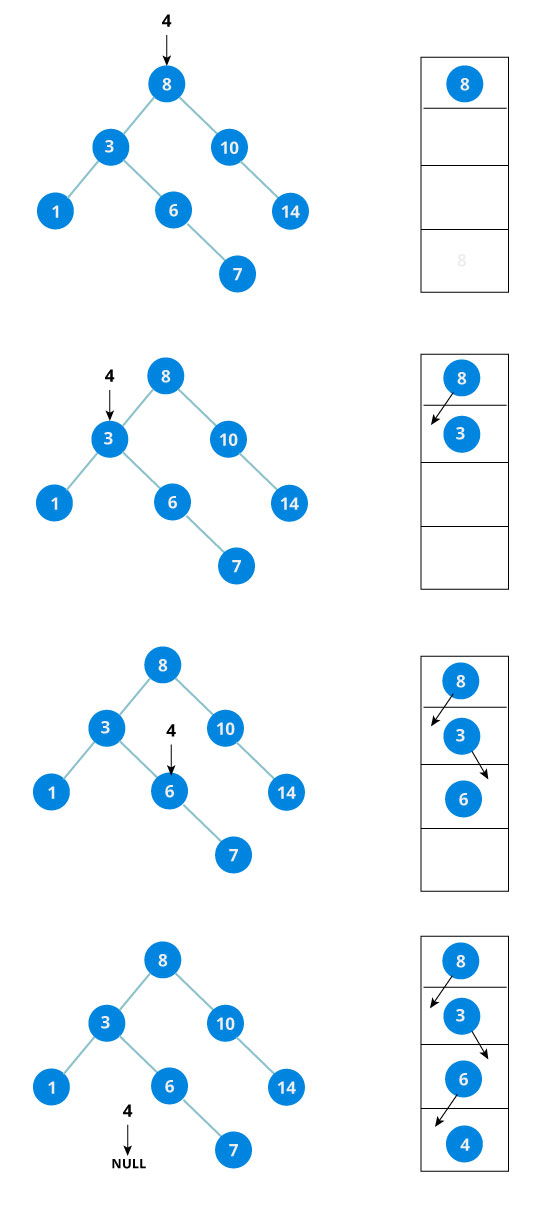
We have attached the node but we still have to exit from the function without doing any damage to the rest of the tree. This is where the return node; at the end comes in handy. In the case of NULL, the newly created node is returned and attached to the parent node, otherwise the same node is returned without any change as we go up until we return to the root.
This makes sure that as we move back up the tree, the other node connections aren't changed.
Time Complexity
The algorithm isn't as simple as it looks. Let's try to visualize how we add a number to an existing BST.

We have attached the node but we still have to exit from the function without doing any damage to the rest of the tree. This is where the return node; at the end comes in handy. In the case of NULL, the newly created node is returned and attached to the parent node, otherwise the same node is returned without any change as we go up until we return to the root.
This makes sure that as we move back up the tree, the other node connections aren't changed.

Here is the example code of insert value in BST in C:
The worst case time complexity of search and insert operations is O(h) where h is height of Binary Search Tree. In worst case, we may have to travel from root to the deepest leaf node. The height of a skewed tree may become n and the time complexity of search and insert operation may become O(n).
Some Interesting Facts
- Inorder traversal of BST always produces sorted output.
- We can construct a BST with only Preorder or Postorder or Level Order traversal. Note that we can always get inorder traversal by sorting the only given traversal.
- Number of unique BSTs with n distinct keys is Catalan Number
LINK TUGAS PROGRAM LINKED LIST ADA DISINI
























Komentar
Posting Komentar